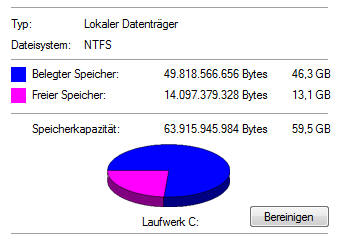
Viele Käufer wundern sich nach dem Anschluss, dass das Betriebssystem für die neue Festplatte nicht so viel Speicher ausweist wie es auf der Verpackung oder im Werbeprospekt stand.

Dateisystem und die Dateiverwaltung benötigen Platz auf der Platte. Mann kann das mit einem Inhaltsverzeichnis vergleichen. Für diese Daten wird ein sogenannter Bootsektor (Master Boot Record oder MBR) angelegt (inklusive Sicherheitskopie des Ganzen), in dem wichtige Informationen für das Verhalten und die Aufteilung der Festplatte oder auch kleine Programme wie ein Boot-Loader  abgelegt sind. Der Boot-Loader hilft dann beim Hochfahren des Rechners das gewünschte Betriebssystem auszuwählen, wenn man mehrere installiert hat. Zum Beispiel Windows XP und Winsows 7 oder wenn Sie Windows 7 installiert haben, aber das neue Windows 8 Beta testen möchten.

Je größer die Kapazität, um so mehr Informationen bezüglich der Dateiverwaltung müssen abgelegt werden. Dafür können schon mal 10 GB flöten gehen oder noch mehr.

Noch ein Grund für den schwindenden Speicher ist, dass Windows seit den letzten Versionen eine "versteckte" Partition anlegt, in der das Betriebssystem wichtige Daten für sich selbst ablegt.

Auch Notebookhersteller und teils sogar PC-Anbieter legen zusätzlich versteckte Partitionen an, die einige GigaByte umfassen können, da sie dort ein Image der kompletten Windowsinstallation mit aller Software samt Werbung und Testversionen ablegen. Das spart zum einen die Herstellung und Mitlieferung von DVDs, zum anderen verlangen die Kunden nach immer flacheren Notebooks, in die keine CD / DVD Laufwerke mehr passen. Fehlende CD Laufwerke sparen auch wieder Kosten und drücken den Preis auf dem hart umkämpften Markt. Externe CD / DVD Laufwerke kauft sich aber kaum jemand. Teuer, unhandlich und immer nicht da wenn man es braucht. Auch für den Kunden ist dies recht bequem. Ist das Betriebssystem im Eimer, drückt man beim Start eine Tastenkombination, bestätigt den Prozess und nach einigen Minuten glänzt das Betriebssystem mit aller Zusatzsoftware wieder wie am ersten Tag.

Der meist diskutierte Grund für den fehlenden Speicherplatz ist die Zählweise.

Im normalen Leben benutzen wir ein Zahlensystem das auf 10 basiert, weil wir 10 Finger haben. Das Dezimalsystem.

Der PC benutzt, in der Technik begründet, ein System auf Basis 2. Das Binärsystem.

Dort ist die kleinste Informationseinheit ein bit. Es kann wie ein Licht 2 Zustände annehmen.

1 oder 0 / an oder aus. Der PC kann also nur mit einem Vielfachen von 2 "rechnen", da es kein halbes bit gibt. Ein Zustand von beiden ist immer vorhanden.

Um 1000 Informationen zu speichern braucht man 10 bit, die jeweils 2 Informationen tragen können. Sie können das leicht Zuhause mit den Nachtischlampen probieren.  > > > > > > >

Haben Sie alle Kombinationen durch, nehmen Sie das Deckenlicht hinzu.

Mit dem ersten bit können 2 Informationen gespeichert werden. Steht das bit auf EINS oder auf NULL. Das ergibt aber noch keine 1000. Wir brauchen ein zweites bit.

Es entstehen die Kombinationen, dass bit2 = NULL haben kann, während das andere, bit1, zur gleichen Zeit = NULL oder EINS besitzen kann. Das sind 2 Möglichkeiten.

Genau diese 2 Möglichkeiten bestehen nun aber auch, wenn das bit2 auf EINS steht. Hier kann das bit1 = wieder seine 2 Zustände einnehmen. EINS oder NULL. Wir haben also 2x zwei Möglichkeiten. Das macht zusammen 4. Das sind aber immer noch keine 1000.

Wir nehmen ein drittes bit. Dieses verdoppelt uns wieder alle vorhergehenden Möglichkeiten, weil alle Zustände zuvor einmal möglich sind wenn dieses dritte bit auf NULL oder, wenn es auf EINS gesetzt ist. Das macht also die 4 Möglichkeiten der vorangegangenen 2 bit einmal wenn das dritte bit Null hat und einmal diese 4 Möglichkeiten, wenn das dritte bit auf EINS ist. Also 2 x4  = 8. Das sind auch noch keine 1000 Informationen. Wir brauchen noch ein bit und noch ein bit.. insgesamt 10 Stück. Siehe folgende Tabelle.

0  -  2  -  4  -  8  -  16  -  32  -  64  -  128  -  256  -  512  -  1024  =  2¹⁰

0 x2 = 0   1 x2 = 2 x2 = 4 x2 = 8 x2 = 16 x2 = 32 x2 = 64 x2 = 128 x2 = 256 x2 = 512 x2 = 1024

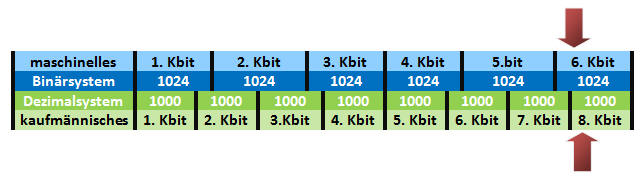
So treffen wir keine 1000, da ein bit weniger nur 512 Möglichkeiten möglich macht, ein bit mehr aber schon 1024 ergibt. Der Pc erreicht also nicht schon bei 1000 die 1000er Marke wie die Kaufmänner und -frauen rechnen, sondern erst bei 1024 und braucht pro 1000 bit die der Hersteller im kaufmännischen Dezimalsystem angibt, 24 bit mehr. Das läppert sich je nach Größe der Festplatte zusammen. Je größer die Festplatte um so mehr "Verlust" hat man. Für den Hersteller / Verkäufer ist dies gut, da es sich mehr anhört. Und es ist auch nicht wirklich falsch.

Wir "verlieren" bei dieser Rechnung also 24 bit pro 1 Kilobit.  Diese 24 bit, die kaufmännisch gesehen zu dem Kilobit danach gehören, fehlen diesem natürlich um selbst auf 1024 zu kommen..

Dem 2. Kilobit dem die 24 bit fehlen, die zum ersten Kbit gefallen sind, fehlen jetzt nicht nur diese 24 um seine eigenen 1024 zusammen zu bekommen, sondern auch noch die 24, die es sich selbst von nächsten genommen hätte. Genau dies tut das 2. Kbit auch und "klaut" sich die 2x 24 Bit vom 3. Kilobit. Es verschiebt sich also schon um 48 bit ins folgende, dem dann wieder diese 48 + seine 24 fehlen. Das nächste Kbit startet schon mit einem "Verlust" von 72 bit und so fort.

Wir "verlieren" bei dieser Rechnung also 24 bit pro 1 Kilobit.